Aproksymacja trygonometryczna

Aproksymacja trygonometryczna

W zagadnieniach aproksymacji często spotykamy się z przypadkiem, gdy funkcja f jest okresowa. Taką funkcję wygodniej i lepiej jest aproksymować nie wielomianami algebraicznymi, a wielomianami trygonometrycznymi . (Jeżeli funkcja f (x) jest funkcją ciągłą o okresie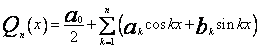 , wielomian trygonometryczny ma postać gdzie są współczynnikami trygonometrycznymi Fouriera funkcji f względem ortogonalnego układu funkcji bazowych[4]. 
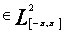Funkcję f ,tzn. funkcję całkowalną z kwadratem aproksymujemy jej sumę Fouriera
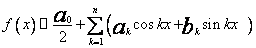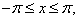, (7)
gdzie
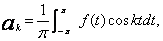k = 0,1,2,...n, (8)
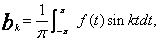k = 1,2,...n. (9)
W przypadku funkcji parzystej:
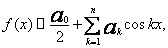
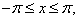(10)
zaś w przypadku funkcji nieparzystej:
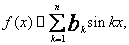
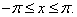(11)
Zachodzi równość
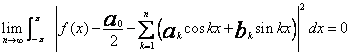(12)
Przykład 1. Aproksymować funkcję 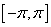w przedziale funkcjami trygonometrycznymi.
Według wzoru (7) otrzymujemy:

gdy k parzyste,
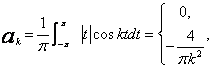gdy k nieparzyste, (13)
a więc
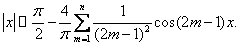(14)
W wielu przypadkach ważna jest nie tylko zbieżność średniokwadratowa (12) szeregu Fouriera (7), a również zbieżność jednostajna. Poniższe dwa twierdzenia podają związek między tymi dwoma rodzajami zbieżności.
Tw. 1.
Ze zbieżności jednostajnej aproksymacji wynika również zbieżność średniokwadratowa tej aproksymacji.
Istnieją różne warunki ( kryteria ), które powinna spełniać funkcja f(x), aby szereg Fouriera był zbieżny jednostajnie. Przytoczę jeden z takich warunków.
Szereg Fouriera funkcji f(x) jest zbieżny do tej funkcji jednostajnie w przedziale 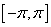, jeśli w nieco szerszym przedziale 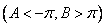funkcja f jest różniczkowalna i ma ograniczoną pochodną [5]