poniedziałek, 2 grudnia 2013

Film przedstawiający kilka programów zawierających wybrane metody numeryczne.
Autor: o Brak komentarzy:
Wideo przedstawiające podstawowe informacje o metodach numerycznych
Autor: o Brak komentarzy:

piątek, 29 listopada 2013

Różne metody analitycznego izolowania pierwiastków

1. Metoda połowienia

Metoda równego podziału (metoda połowienia, metoda bisekcji, metoda połowienia przedziału) – jedna z metod rozwiązywania równań nieliniowych. Opiera się ona na twierdzeniu Bolzano-Cauchy’ego:
Jeżeli funkcja ciągła f(x) ma na końcach przedziału domkniętego wartości różnych znaków, to wewnątrz tego przedziału, istnieje co najmniej jeden pierwiastek równania f(x)=0.
Aby można było zastosować metodę równego podziału, muszą być spełnione założenia:
  1. funkcja f(x) jest ciągła w przedziale domkniętym [a;b]
  2. funkcja przyjmuje różne znaki na końcach przedziału: f(a)f(b)<0
Przebieg algorytmu:
  1. Sprawdzić, czy pierwiastkiem równania jest punkt x_1=\frac{a+b}{2}, czyli czy f(x_1)=0.
  2. Jeżeli tak jest, algorytm kończy się, a punkt jest miejscem zerowym. W przeciwnym razie x_1 dzieli przedział [a,b] na dwa mniejsze przedziały [a, x_1] i [x_1, b].
  3. Wybierany jest ten przedział, dla którego spełnione jest drugie założenie, tzn. albo f(x_1)f(a) < 0 albo f(x_1)f(b) < 0. Cały proces powtarzany jest dla wybranego przedziału.
Działanie algorytmu kończy się w punkcie 2 albo po osiągnięciu żądanej dokładności przybliżenia pierwiastka.

2. Regula falsi

Regula falsi (łac. fałszywa linia prosta, fałszywa reguła) — algorytm rozwiązywania równań nieliniowych jednej zmiennej.
Na funkcję y=f(x) nakładane są następujące ograniczenia:
  1. W przedziale [a,b] znajduje się dokładnie jeden pojedynczy pierwiastek.
  2. Na końcach przedziału funkcja ma różne znaki: f(a)f(b) < 0.
  3. Pierwsza i druga pochodna istnieją i mają na tym przedziale stałe znaki.
Algorytm przebiega następująco:
  • Na początku przez punkty A=(a, f(a)) i B=(b, f(b)) przeprowadzana jest cięciwa.
  • Punkt przecięcia x_1 z osią OX jest brany jako pierwsze przybliżenie pierwiastka.
  • Jeśli to przybliżenie jest wystarczająco dobre, algorytm kończy się.
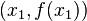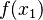  • Jeśli nie, to prowadzona jest cięciwa przez punkty (x_1, f(x_1)) oraz A lub B – wybierany jest ten punkt, którego rzędna ma znak przeciwny do f(x_1). Jednak w praktyce, dzięki ograniczeniu nr 3 już na początku algorytmu wiadomo, który z tych punktów będzie stały, tzn. wybierany za każdym razem.
  • Następnie wyznaczane jest przecięcie nowo wyznaczonej cięciwy z osią OX (x_i) i algorytm powtarza się.
Nazwa metody pochodzi od łacińskich słów: regula1 znaczące zarówno linię prostą, jak i regułę i falsus, fałszywy — metoda bazuje na fałszywym twierdzeniu (regule), że na pewnym przedziale funkcja jest liniowa. Można więc tę nazwę przetłumaczyć zarówno jako "fałszywa linia prosta" jak i "fałszywa reguła" i obydwa te tłumaczenia mają w tym kontekście sens.

Wzory

x_{1}=\frac{af(b)-bf(a)}{f(b)-f(a)}
x_{i+1}=\left\{\begin{matrix} \frac{x_i f(a) - a f(x_i)}{f(a) - f(x_i)} & gdy &f(a)f(x_i)\le 0 \\ \\ \frac{x_i f(b) - b f(x_i)}{f(b) - f(x_i)} & gdy&f(b)f(x_i)<0 \end{matrix}\right.
dla i=1,2,...

3. Metoda siecznych 

Metoda siecznych (metoda Eulera) — metoda numeryczna, służąca do rozwiązywania równań nieliniowych z jedną niewiadomą.
Metoda siecznych to algorytm interpolacji liniowej. Polega na przyjęciu, że funkcja na dostatecznie małym odcinku <a,b> w przybliżeniu zmienia się w sposób liniowy. Możemy wtedy na odcinku <a,b> krzywą y=f(x) zastąpić sieczną. Za przybliżoną wartość pierwiastka przyjmujemy punkt przecięcia siecznej z osią OX.
Metodę siecznych dla funkcji f(x), mającej pierwiastek w przedziale <a,b> można zapisać następującym wzorem rekurencyjnym:
\left\{ \begin{matrix} x_{0} = a & \\ x_{1} = b & \\ x_{n+1} = x_{n} - \frac{f(x_{n})(x_{n}-x_{n-1})}{f(x_{n})- f(x_{n-1})} & n=1,2,\ldots \\ \end{matrix} \right.
Metoda siecznych ma tę zaletę, że do wykonania interpolacji za jej pomocą niepotrzebna jest znajomość pochodnych funkcji (odwrotnie niż np. w metodzie Newtona). Z drugiej strony, gdy wybierzemy zbyt mały przedział [a,b] metoda ta może nie być zbieżna, np.:
\left\{ \begin{matrix} a = 0.5 & \\ b = 1 & \\ f(x) = 2x - x^3-1 \\ \end{matrix} \right.
W powyższym przypadku na zmianę będziemy otrzymywali pierwiastki równe 0,5 lub 1. Gdy metoda siecznych nie prowadzi do wyniku, warto zastosować metodę alternatywną.

 

Autor: o Brak komentarzy:

Aproksymacja trygonometryczna

Aproksymacja trygonometryczna

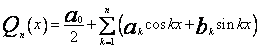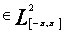W zagadnieniach aproksymacji często spotykamy się z przypadkiem, gdy funkcja f jest okresowa. Taką funkcję wygodniej i lepiej jest aproksymować nie wielomianami algebraicznymi, a wielomianami trygonometrycznymi . (Jeżeli funkcja f (x) jest funkcją ciągłą o okresie , wielomian trygonometryczny ma postać gdzie są współczynnikami trygonometrycznymi Fouriera funkcji f względem ortogonalnego układu funkcji bazowych[4]. 
Funkcję f ,tzn. funkcję całkowalną z kwadratem aproksymujemy jej sumę Fouriera
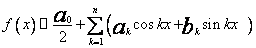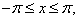, (7)
gdzie
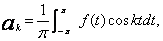k = 0,1,2,...n, (8)
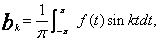k = 1,2,...n. (9)
W przypadku funkcji parzystej:
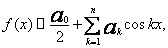
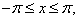(10)
zaś w przypadku funkcji nieparzystej:
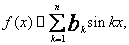
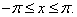(11)
Zachodzi równość
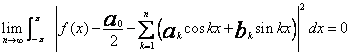(12)
Przykład 1. Aproksymować funkcję 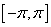w przedziale funkcjami trygonometrycznymi.
Według wzoru (7) otrzymujemy:

gdy k parzyste,
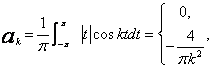gdy k nieparzyste, (13)
a więc
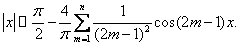(14)
W wielu przypadkach ważna jest nie tylko zbieżność średniokwadratowa (12) szeregu Fouriera (7), a również zbieżność jednostajna. Poniższe dwa twierdzenia podają związek między tymi dwoma rodzajami zbieżności.
Tw. 1.
Ze zbieżności jednostajnej aproksymacji wynika również zbieżność średniokwadratowa tej aproksymacji.
Istnieją różne warunki ( kryteria ), które powinna spełniać funkcja f(x), aby szereg Fouriera był zbieżny jednostajnie. Przytoczę jeden z takich warunków.
Szereg Fouriera funkcji f(x) jest zbieżny do tej funkcji jednostajnie w przedziale 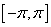, jeśli w nieco szerszym przedziale 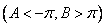funkcja f jest różniczkowalna i ma ograniczoną pochodną [5]
Autor: o Brak komentarzy:
Subskrybuj: Posty (Atom)